The RIT Discrete and Computational Mathematics Seminar
Overview
Welcome to the Discrete and Computational Mathematics Seminar at RIT (DisCoMathS)! We are a big tent seminar series for everything discrete: graph theory, combinatorics, combinatorial optimization, applications of discrete mathematics, and computational aspects of all these subjects. During the Spring 2025 semester the seminar meets most weeks (see the schedule below for the exact dates) in the Sustainability Institute Hall (SUS-3140). All talks are scheduled from 3:00PM until 3:50PM Rochester time on Mondays (unless otherwise noted). We encourage you to join us in person, but if you are unable to join us the talks are also streamed via Zoom. For seminar announcements, schedule updates, and Zoom links, be sure to subscribe to the mailing list (see below).
DisCoMathS is open to the public, and everyone is welcome to attend. Graduate and undergraduate students are especially welcome.
The seminar is organized this semester by Brendan Rooney. If you would like to give a seminar, please contact discomaths@rit.edu.
Mailing List
Seminar communications (announcements, scheduling polls, etc.) will be sent via the DisCoMathS mailing list. Join now!
Past Seminars
Monday, March 3
Speaker: Darren Narayan
Title: Mathematical Jigsaw Puzzles
Abstract: We consider the problem of tiling large rectangles using smaller rectangles with the prescribed dimensions $4\times 6$ and $5\times 7$. Problem B-3 on the 1991 William Lowell Putnam Examination asked "Does there exist a natural number $L$ such that if $m$ and $n$ are integers greater than $L$, then an $m\times n$ rectangle may be expressed as a union of $4\times 6$ and $5\times 7$ rectangles, any two intersect at most along their boundaries?" Narayan and Schwenk showed in 2002 that all rectangles with length and width at least $34$ can be partitioned into $4\times 6$ and $5\times 7$ rectangles. We investigate necessary and sufficient conditions for an $m \times n$ rectangle to be tiled with $4\times 6$ and $5\times 7$ rectangles, using techniques from algebra, combinatorics, and integer linear programming.
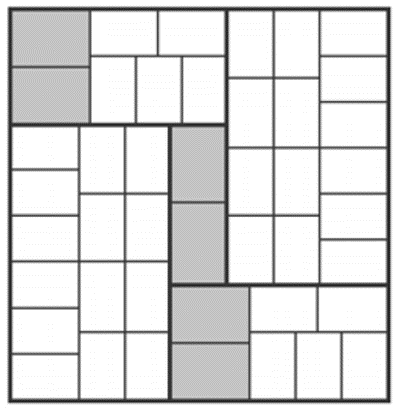
Monday, March 17
Speaker: Bonnie Jacob
Title: Applying Wellness to Zero Forcing and Failed Zero Forcing
Abstract: Well-covered and well-dominated graphs, graphs in which every minimal vertex cover and every minimal dominating set has the same cardinality respectively, were investigated starting a few decades ago. More recently, there has been an effort to apply the “well” idea to zero forcing. We will discuss well-forced and well-failed graphs, which are graphs in which every minimal zero forcing set is a minimum zero forcing set, and every maximal failed zero forcing set is a maximum failed zero forcing set, respectively. We'll also discuss some recent related work.
Monday, March 24
Speaker: Kristijan Tabak
Title: Cubes of Symmetric Designs and Group Actions
Abstract: A 3-dimensional cube of a symmetric $(v, k, λ)$-design is a map from $[v]^3$ to $\{0, 1\}$ such that every slice of a cube is an incidence matrix of a $(v, k, λ)$-symmetric design. We analyze a regular action of a group $G$ of order $v$ on slices of a cube. We generalize classical results about regular action of a group on a symmetric design to a case of a dimension 3. Additionally, we prove that a group action on one set of parallel slices fully determines an action of $G$ on other perpendicular slices. We also prove that it is not possible to have parallel slices as left and right $G$-orbits simultaneously. Furthermore, we prove that possible $G$ orbits of mutually perpendicular slices alternate in a sense of being a left and right $G$-orbit.
Monday, March 31
Speaker: Tess Collins (RIT)
Title: Quantum Colorings of Graphs
Abstract: Graph coloring is one of the most well-known areas of graph theory, and the seductiveness of a graph's chromatic number has incited many extensions and relaxations of this parameter. One such extension is the "quantum chromatic number" of a graph, denoted $\chi_q(G)$. In a quantum $c$-coloring of a graph $G$, each vertex is assigned a set of $c$ orthogonal projectors such that two important properties are satisfied: 1) Completeness: the matrices assigned to each vertex sum to the identity, and 2) Orthogonality: respective matrices of adjacent vertices are orthogonal. We will talk about the "physics-y" origin of this version of graph coloring, look at some fun examples and known properties of quantum colorings of graphs, discuss the two existing methods for constructing a quantum coloring of a graph, and touch on how we might extend these methods.
Monday, April 7
Speaker: Jason LaRuez (RIT)
Title: Analyzing Networks and Hypernetworks with Topology
Abstract: In recent years, topological data analysis has been used with great success to analyze the structure of complex high-dimensional data, merging methods from data science and computational topology. We will discuss the approaches typically used to convert networks (graphs) and hypernetworks (hypergraphs) into simplicial complexes, which allow us to extract topological properties and quantities. This will be followed by a discussion of applications of these methods, including those in neuroscience and cybersecurity. Finally, we will introduce a generative hypergraph model that attempts to generalize the classical Barabási-Albert network model, concluding with preliminary topological results.
Monday, April 14
Speaker: Dominick Banasik (RIT)
Title: Energy-Efficient Initialization in Single-Hop Radio Networks
Abstract: Initialization is the problem of assigning unique, consecutive identifiers to every processor in a radio network. This is of particular interest in single-hop networks because once initialized, the processors can communicate without collisions. Nakano and Olariu (2000) introduced an energy-efficient initialization algorithm for single-hop radio networks with sender-side feedback, in which no node is awake for more than $O(\log \log n)$ timesteps.
We study the problem of partial initialization, in which we aim to initialize a constant fraction of the nodes, in the more challenging setting with no sender-side feedback. We present an algorithm for solving partial initialization energy in radio networks with no collision detection or sender-side feedback with probability at least $1 - \exp(-n^{1 - \varepsilon})$. Our algorithm runs in linear time and has an energy complexity of $O(\log^* n)$. As a consequence of solving partial initialization, we can solve initialization without sender-side feedback while maintaining the $O(\log \log n)$ energy bound.
Monday, April 21
Speaker: Varsha Dani
Title: On the Instance Complexity of Set Intersection
Abstract: Typically, when analyzing algorithmic performance, we focus on worst-case complexity, where the goal is to optimize a time complexity function $T(n)$, defined as the maximum running time over all inputs of length $n$. In Instance Complexity, however, one seeks a much more fine-grained notion of optimality, where the time complexity function $T(x)$ is defined over all input strings, $x$. An algorithm is said to have optimal instance complexity, if, for every possible input, its running time is the best possible for that input. Surprisingly, there are some settings in which it is possible to design nearly optimal algorithms, even with this much more refined notion of optimality.
Motivated by the problem of Join Queries in Distributed Databases, we study the following version of the Set Intersection problem in communication complexity. Each of $n$ players is given a subset of a universe $\{1, 2, \ldots , N\}$. After a communication protocol, every player should know the intersection of all $n$ sets. We give a nearly instance-optimal algorithm for this problem under some fairly natural restrictions to the type of algorithm that is allowed. The key idea comes from the answer to a popular math riddle known as a "rope-burning puzzle".
Joint work with Tom Hayes and Atri Rudra, both at University at Buffalo.
Wednesday, February 28
Speaker: Garrison Koch (RIT)
Title: On the $n$-attack Roman Dominating Number of a Graph and the use of End-Connected Center-Disjoint $P_5$ subgraphs
Abstract: The Roman Dominating number is a widely studied variant of the dominating number on graphs. Given a graph $G=(V,E)$, the dominating number of a graph is the minimum size of a vertex set, $V' \subseteq V$, so that every vertex in the graph is either in $V'$ or is adjacent to a vertex in $V'$. The Roman Dominating function of $G$ is defined as $f:V \rightarrow \{0,1,2\}$ such that every vertex with a label of 0 in $G$ is adjacent to a vertex with a label of 2. The Roman Dominating number of a graph is the minimum total weight over all possible Roman Dominating functions. In this talk we analyze a new variant: $n$-attack Roman Domination, particularly focusing on 2-attack Roman Domination $(n=2)$. The $n$-attack Roman Dominating function of $G$ is defined similarly to the Roman Dominating function with the additional condition that for any $j\leq n$, any subset $S$ of $j$ vertices all with label 0, must have at least $j$ vertices with label 2 in the open neighborhood of $S$. The $n$-attack Roman Dominating number is the minimum total weight over all possible $n$-attack Roman Dominating functions. We introduce a method for finding the 2RD number of a graph. We touch on extensions such as infinite regular graphs and "finite resources". We conclude with open questions and possible ways to extend these results to the general $n$-attack case.
Wednesday, March 6
Speaker: Kristijan Tabak
Title: Hadamard cubes and permutation invariant sums over finite fields
Abstract: We will introduce Hadamard cubes over finite fields. We will analyze specific sums that appear in some constructions, and which are invariant on an action of a permutation group $S_3$.
Wednesday, March 20
Speaker: Mary Lynn Reed
Title: Irrational Randomness (with some cool graphs, too)
Abstract: One of the earliest (possibly the very first) pseudo-random number generator (PRNG) is von Neumann’s “Middle-Square” method. It’s fun to play with, and it’s super-fast computationally, but it turns out to be an awful PRNG. In this talk we’ll have a look at some of the cool graph structures that result from the “awfulness” of the original Middle Square method; and we’ll describe a recent revival of the Middle-Square method that incorporates Weyl sequences to make for a much stronger PRNG. This talk has minimal pre-requisites and will touch on several “further areas of exploration” that could make for some cool research projects (even at the undergraduate level).
Wednesday, April 10
Speaker: Bonnie Jacob
Title: Well, well, well... "well"ness in graph theory, especially well-forcedness
Abstract: Many graph problems focus on finding the minimum value of a particular kind of vertex set on a graph. For example, finding minimum vertex covers or minimum dominating sets are non-trivial problems. For a few of these parameters, researchers have considered what graphs have the interesting property that every minimal $X$-set (where $X$ is your favorite minimizable graph parameter) is also a minimum $X$-set, and call such graphs well $X$ed.
We start this talk by briefly looking at some examples of "well"ness among different parameters before delving into our research that applied this well idea to zero forcing. In our work, we introduced the concept of well-forced graphs, that is, graphs in which every minimal zero forcing set is a minimum zero forcing set. We were able to characterize well-forced trees, and along the way discovered some interesting properties of vertices that appear in no minimal zero forcing sets. We describe our results here and some open questions.
Wednesday, April 17
Speaker: Varsha Dani
Title: Fraud Detection for Random Walks
Abstract: Traditional fraud detection is often based on finding statistical anomalies in data sets and transaction histories. A sophisticated fraudster, aware of the exact kinds of tests being deployed, might be difficult or impossible to catch. We are interested in paradigms for fraud detection that are provably robust against any adversary, no matter how sophisticated. In other words, the detection strategy should rely on signals in the data that are inherent in the goals the adversary is trying to achieve.
Specifically, we consider a fraud detection game centered on a random walk on a graph. We assume this random walk is implemented by having a player at each vertex, who can be honest or not. In particular, when the random walk reaches a vertex owned by an honest player, it proceeds to a uniformly random neighbor at the next timestep. However, when the random walk reaches a dishonest player, it instead proceeds to an arbitrary neighbor chosen by an omniscient Adversary.
The game is played between the Adversary and a Referee who sees the trajectory of the random walk. At any point during the random walk, if the Referee determines that a specific vertex is controlled by a dishonest player, the Referee accuses that player, and therefore wins the game. The Referee is allowed to make the occasional incorrect accusation, but must follow a policy that makes such mistakes very unlikely. The goal of the adversary is to delay the cover time, defined as the number of timesteps until all vertices of the graph have been visited at least once.
We consider the following basic question: how much can the omniscient Adversary delay the cover time without getting caught? Our main result is a tight upper bound on this delay factor.
Joint work with Tom Hayes, Seth Pettie, and Jared Saia.
Paper link: https://drops.dagstuhl.de/entities/document/10.4230/LIPIcs.ITCS.2024.36
Wednesday, April 24
Speaker: Matt Coppenbarger
Title: Strategy Stealing Games
Abstract: In combinatorial game theory, a strategy-stealing argument shows that, for a two-person game, the first player has a guaranteed winning strategy. The argument was invented by John Nash in the 1940s to show that the game Hex is always a first-player win. The main discussion of the talk will be on two games, Chomp and Bridg-It. Some additional games may be discussed.
Tuesday, February 14
Speaker: Brendan Rooney
Title: Cyclotomic Matrices and Graphs with $q=2$
Abstract: We survey a sequence of papers by Smyth, McKee, Greaves, and Taylor (see [1], [2], [3], [4], [5], [6]) on Lehmer's Conjecture and cyclotomic matrices. Our focus is the graphs corresponding to maximal indecomposable cyclotomic matrices (GMICs for short).
For a graph $G$, the value $q(G)$ is the smallest number of distinct eigenvalues of a symmetric matrix $M$ whose off-diagonal zero pattern matches that of the adjacency matrix of $G$ exactly. Recent work on sparse graphs, and $4$-regular graphs, with $q(G)=2$ reveals that most of these $q=2$ graphs correspond to GMICs. This talk is part of an attempt to connect these bodies of work, and will contain open questions.
Tuesday, February 28
Speaker: Zohair Hassan (RIT)
Title: On the hardness of $(P_3, H)$-Non-Arrowing
Abstract: Graph arrowing is concerned with determining which monochromatic subgraphs are unavoidable when coloring a given graph. The complexity of various arrowing problems has been studied for decades, particularly when the subgraphs to be avoided are fixed. Some cases have been shown to be solvable in polynomial time or NP-complete. We focus on the latter case.
In this presentation, we will focus on $(P_3, H)$-Non-Arrowing; determining whether it is possible to color a given graph's edges red or blue such that there are no red $P_3$'s or blue $H$'s, where $P_3$ is the path graph on three vertices, and $H$ is a fixed graph. In particular, we will observe how structural properties (e.g., $k$-connectivity) of $H$ allow us to construct gadgets to reduce a variant of SAT to the $(P_3, H)$-Non-Arrowing problem. This provides hardness results for an infinitely large family of $H$.
Tuesday, March 21
Speaker: Matt Coppenbarger
Title: Oodles and oodles of googols: Iterations of the Words-to-Numbers Function
Abstract: The Words-to-Numbers function takes a nonnegative integer and maps it to the number of characters required to spell the number in English. For each $k=0,1,\ldots,8$, we determine the minimal nonnegative integer $n$ such that the iterates of $n$ converge to the fixed point (through the Words-to-Numbers function) in exactly $k$ iterations. Our travels take us from some simple answers, to an etymology of the names of large numbers, to Conway/Guy's established system representing the name of any integer, and finally use generating functions to arrive at a very large number.
Tuesday, March 28
Speaker: Kristijan Tabak
Title: Cubes of designs
Abstract: A symmetric design is a combinatorial object represented as a matrix with entries 0 and 1, where any two rows and any two columns have equal number of ones on respective locations. Historically, symmetric designs were studied in genetics and in designs of pharmaceutical experiments. Afterwards, it became a mainstream part of mathematics.
In this talk we shall represent new developments in a theory of multidimensional symmetric designs that was originated by dr. Krčadinac, dr. Pavčević and dr. Tabak. In brief, we study 3-dimensional, 4-dimensional etc. cubes of (0,1) matrices that preserve a great deal of symmetry inherited from a basic 2-dimensional case.
Applications of cubes of designs are possible in a complex setting of statistical tests, neural networks, optimization problems etc.
Tuesday, April 4
Speaker: Kristijan Tabak
Title: Surprising dualities of incidence structures across finite vector spaces
Abstract: A natural generalization of a symmetric design is usually made within the frame of a vector space over the finite field. With this in mind, we present new dualities in a ‘min-max’ way, meaning that some minimal substructures in a vector space (over finite field) are deeply related with the appropriate maximal structures in the same ambient space. Both ‘extremes’ are constructed using generalizations of a symmetric design and also, what it seems now, not related with classical concepts of residual or derived designs. This is still work in progress. We believe that this could yield to some new algebraic identities that may be interpreted as ‘Mobius like’ inversion formulas that we have seen in number theory.
Tuesday, April 11
Speaker: Darren Narayan
Title: Failed Zero Forcing Numbers of Graphs
Abstract: Given a graph $G$, the zero forcing number of $G$, $Z(G)$, is the smallest cardinality of any set $S$ of vertices on which repeated applications of the forcing rule results in all vertices being in $S$. The forcing rule is: if a vertex $v$ is in $S$, and exactly one neighbor $u$ of $v$ is not in $S$, then $u$ is added to $S$ in the next iteration. Zero forcing numbers have attracted great interest over the past 15 years and have been well studied. In this paper, we investigate the largest size of a set $S$ that does not force all of the vertices in a graph to be in $S$. This quantity is known as the failed zero forcing number of a graph and will be denoted by $F(G)$. We present new results involving this parameter.
Tuesday, April 18
Speaker: Shahla Nasserasr
Title: On the Inverse Eigenvalue Problem and Distinctness of Eigenvalues
Abstract: Consider the set all $n\times n$ real symmetric matrices where all of them follow a fixed pattern of zero-nonzero entries on their off-diagonal entries. The inverse eigenvalue problem then asks to determine all possible spectra of such matrices. The question is difficult and one way to relax it is to study the minimum number of distinct eigenvalues instead of the values of the eigenvalues. This parameter is denoted by $q(G)={\rm min}\{q(A)|A \in \mathcal{S}(G)\}$ where $G$ is a graph that represents the pattern of the set of matrices. In this presentation, I will review some of the results and the techniques from recent developments about $q(G)$.
Wednesday, September 14
Speaker: Brendan Rooney
Title: How to Draw a Graph Pt 1
Abstract: We review some properties of the Laplacian matrix of a graph, and show how it can be used to draw graphs in the plane.
Wednesday, September 21
Speaker: Brendan Rooney
Title: How to Draw a Graph Pt 2
Abstract: We continue our discussion of graph drawings using the Laplacian matrix. In this seminar we will see Tutte's method for drawing 3-connected planar graphs, and Steinitz's Theorem on convex polyhedra in $\mathbb{R}^3$.
Wednesday, September 28
Speaker: Matthew Coppenbarger
Title: The Principle of Parity in Analyzing Puzzles
Abstract: The mathematical principle of parity is the simple and obvious fact that an even number is not equal to an odd number. It is a powerful tool that is usually restricted for use in impossibility proofs, but it can also be used as a way to make some very challenging puzzles where the solutions utilize the principle of parity.
This talk will cover many puzzles, starting with the well-known The Puzzle of 15, the impossibility of the 14-15 Puzzle, and a few other sliding block puzzles. In addition, half a dozen construction puzzles using various polyform pieces will be introduced, including a more elaborate version of the Soma Cube. Lastly, a brief discussion of the Eternity Puzzle. This last puzzle originated in the Britain and offered a $1.4 million prize to the first person or persons to produce a complete solution.
Solutions of most puzzles will not be provided, but clues on how to find the solution will be given. A number of the discussed puzzles will be available after the talk. No special knowledge of mathematics is needed to understand the material presented.

Wednesday, October 12
Speaker: Shahla Nasserasr
Title: Zero Forcing Game and Some of Its Variants
Abstract: Zero forcing of a graph is a color-change rule on the vertices of the graph using two colors. This a one-player game and the goal is to color all of the vertices with the same color (following the rules). The color-change rule and the number of players can vary depending the underlying problem and matrices. In this talk we will review some variants of zero forcing and their properties.
Wednesday, November 2
Speaker: Bonnie Jacob
Title: Two problems in power domination
Abstract: What is the most efficient way to successfully place phasor measurement units (PMUs) on an electric power grid? The graph theoretic approach to modeling this problem is known as power domination. Mathematically speaking, power domination has a great deal in common with the well-known graph theory areas of domination and zero forcing, and interestingly, was introduced earlier than zero forcing. In this talk, I will talk about failed power domination which is the study of how many PMUs can be placed on the grid without effectively monitoring the grid, as well as power domination reconfiguration, which is the investigation of when one PMU configuration can be changed into another under certain constraints.
Wednesday, November 16
Speaker: Hossein Shahmohamad
Title: Graphs and Their Potent Energy Drinks
Abstract: Energy of a graph was defined by Gutman in 1978 and originates from theoretical chemistry. For an $n$-vertex graph $G$ with adjacency matrix $A$ having eigenvalues $\lambda_1\geq\lambda_2\geq\ldots\geq\lambda_n$, the energy $E(G)$ is defined as the sum of absolute values of all eigenvalues, i.e., $E(G)=\sum_{i=1}^n|\lambda_i|$. This is related to the total $\pi$-electron energy in a molecule represented by a graph. Origins of this topic are found in Hückel molecular orbital theory (HMO), $\pi$-electrons and their total energy $E_{\pi}$, molecular orbital energy levels $E_j$, the HMO Hamiltonian operator. The term “energy” comes from quantum Chemistry. The study of graph energy is deeply related to modeling of spread of epidemics, properties of proteins, the search for the genetic causes of Alzheimer disease, and entropy. In this talk, we compile and summarize many of the recent discoveries and progress made on this topic.

February 9
Speaker: Brendan Rooney
Title: Graphs with Few Eigenvalues
Abstract:A graph $G$ has several matrices associated with it: its adjacency matrix; its Laplacian matrix; its Laplacian matrix; and, its Seidel matrix. All of these are well-studied. We will look at graphs for which these matrices have a small number of distinct eigenvalues. We will see some of the classical theory of strongly regular graphs. The results of Haemers and Omidi on eigenvalues of the universal adjacency matrix of $G$ will be discussed.
February 16
Speaker: Hannah Miller
Title: Enumerating Nontrivial Knot Mosaics with SAT
Abstract:Mathematical knots are interesting topological objects. Using simple arcs, lines, and crossings drawn on eleven possible tiles, knot mosaics are a representation of knots on a mosaic board. Our contribution is using SAT solvers as a tool for enumerating nontrivial knot mosaics. By encoding constraints for local knot mosaic properties, we computationally reduce the search space for small mosaics by factors of up to 6600. Our future research directions include attacking larger mosaics with parallel SAT techniques and studying the behavior of ALLSAT solvers on our knot mosaics SAT formula.
March 2
Speaker: Brendan Rooney
Title: Equiangular Lines
Abstract:We survey some of the theory on equiangular sets of lines. Our focus will be on Seidel matrices, with an eye to finding useful expressions of matrices in $\mathcal{S}(K_n)$ as Gram matrices. We will also see connections to strongly regular graphs.
March 16
Speaker: Zohair Hassan
Title: On the Hardness of Graph Arrowing: A Combinatorial Computing Approach Part 1
Abstract: Graph arrowing is concerned with determining which monochromatic subgraphs are unavoidable when coloring a given graph. The complexity of various arrowing problems has been studied for decades, particularly when the subgraphs to be avoided are fixed. Some cases have been shown to be solvable in polynomial time or to be coNP-complete. We focus on the latter case. Previous hardness proofs typically rely on ad-hoc, laborious constructions of "gadgets." We propose searching for gadgets computationally. These gadgets will allow us to simulate variants of SAT, thus showing coNP-hardness.
In this presentation, we will focus on $P_3P_5$-Arrowing; determining whether it is possible to color a given graph's edges red or blue such that there are no red $P_3$'s or blue $P_5$'s, where $P_n$ is the path graph on $n$ vertices. We will show that $P_3P_5$-Arrowing is coNP-complete by discussing the properties of gadgets that may be used in a proof.
March 23
Speaker: Zohair Hassan
Title: On the Hardness of Graph Arrowing: A Combinatorial Computing Approach Part 2
Abstract: We previously explored $P_3P_5$-Arrowing and how one could prove its coNP-hardness with the right gadgets. In this presentation, we will explore how to find these gadgets computationally. Our approach is based on enumerating over a set of generated candidate graphs until we find one that meets the requirements of our gadget.
We will discuss a general framework that can be implemented to generate candidate graphs, and how this framework can be made more efficient. This will be followed by a presentation of the results, showcasing the gadgets found and the complete proof. Finally, we will discuss the applicability of this approach to other graph arrowing problems.
March 30
Speaker: John Mooney
Title: Numerically Balanced Dice
Abstract: Dice can only be fair in theory due to various physical imperfections that inevitably occur during manufacturing processes. A die is considered numerically balanced despite physical imperfections when the numbers assigned to its faces satisfy sets of linear constraints to preserve a fair die's expected value. The existence of numerically balanced dice was first confirmed in Bosch et al. using integer programming techniques to find balanced numberings of the d20, d30, and d120. We explore how to answer questions regarding uniqueness (up to isomorphism) of some isohedra suitable for use as fair dice. In this talk, we discuss the combinatorics involved to make the problem more computationally tractable and as well as approaches that eliminate the need for computation altogether. We present 5 new non-isomorphic numerically balanced numberings of the d20 (regular icosahedron).
April 13
Speaker: Matt Coppenbarger
Title: Maximal Heights of the Bulgarian Solitaire Function
Abstract: The Bulgarian Solitaire function, introduced nearly 40 years ago by Martin Gardner, is a function on integer partitions. It is best modeled by a deck of cards (or any collection of indistinguishable counters - coins work too). The cards are divided into any number of stacks. The function takes a single counter from each stack and forms a new stack (and so stacks with a single counter disappear when the counter is removed). The process is iterated over and over to see what happens. The talk will go through the main results and the open question that I've been working on for a few years.
September 17
Speaker: Shahla Nasserasr
Title: Rigid Linkages and Eigenvalues
Abstract: Given an assignment of colours blue and white to the vertices of graph $G$, the zero forcing rule determines a subset of white vertices to be re-coloured blue. The zero forcing process applies this rule in discrete time-steps until no more changes are possible. Rigid linkage forcing is defined similarly to the standard zero forcing process. Rigid linkages are used to provide more information on the multiplicities of the eigenvalues, and the relationship between the eigenvalues of matrices related to graphs.
In this talk, some properties and applications of the rigid linkage forcing process will be discussed.
September 24
Speaker: Brendan Rooney
Title: Combinatorial Orthogonality and Graphs with $q=2$
Abstract: Two vectors are combinatorially orthogonal if the size of the intersection of their supports is not 1. An $n\times n$ symmetric matrix is combinatorially orthogonal if every pair of rows, or columns, is combinatorially orthogonal. Every orthogonal pair of vectors is combinatorially orthogonal, and every orthogonal matrix is combinatorially orthogonal. For a graph $G$, we give a simple structural condition that guarantees the existence of a combinatorially orthogonal matrix in $\mathcal{S}(G)$ (the set of symmetric matrices with the same off-diagonal zero-pattern as the adjacency matrix of $G$). We will see how this connects with work done by Reid and Thomassen on graphs for which every path of length $r$ is contained in a cycle of length $s$. Finally we discuss implications for finding $q(G)$, and characterizing graphs with $q=2$.
October 1
Speaker: Bonnie Jacob
Title: >Bringing Together Zero Forcing and Failed Zero Forcing: The Zero Forcing Span of a Graph
Abstract:Between the zero forcing number of a graph $\mbox{Z}(G)$ and the failed zero forcing number $\mbox{F}(G)$ is where anything can happen. More specifically, if $\mbox{Z}(G) \leq k < \mbox{F}(G)$, there exist sets of cardinality $k$ that are zero forcing sets, and sets of cardinality $k$ that are not. For some graphs, there are many such cardinalities (or equivalently, the difference between $\mbox{Z}(G)$ and $\mbox{F}(G)$ is large), while for others, there are none. We call the number of such cardinalities the zero forcing span of a graph. In this talk, we connect results on $\mbox{Z}(G)$ with results on $\mbox{F}(G)$ to describe graphs that have various zero forcing spans, providing characterizations of some extreme values.
October 8
Speaker: Kristijan Tabak (RIT Croatia)
Title: Binary Fano Plane and Automorphisms of Order 7
Abstract: The binary Fano plane is a combinatorial design embedded in 7-dimensional finite vector space over $GF(2)$. The blocks are made of 3-dimensional subspaces so that any 2-dimensional space is a subspace of just one block. It is still unknown whether such a design exists. What is known is that (among others) an automorphism of order 7 can’t operate on a set of blocks. This was proved by extensive use of computer power.
Here we present the first algebraic computer-free proof of that fact. The methods used in the proof involve group theory, character theory and calculations in various group rings.
October 15
Speaker: Peter Maceli (Ithaca College)
Title: Chi-boundedness
Abstract: If a graph has bounded clique number, and sufficiently large chromatic number, what can we say about its induced subgraphs? In the early 1980's András Gyárfás made a number of challenging conjectures about this. In this talk, we will give a brief survey of how these questions seek to generalize the class of perfect graphs, along with some recent results.
October 22
Speaker: Kristijan Tabak (RIT Croatia)
Title: On $p$-Groups with Minimal Subgroup Centralizers - New Results
Abstract: We present new results on a problem of $CZ_p$-groups (i.e., groups $G$ for which the centralizer of any subgroup is the center of $G$). Such groups are highly nonabelian. The results presented here will be a natural continuation of previously published results where we have proved that such groups have at least $p^5$ elements. We make new connections between $CZ_p$-groups and groups of maximal class.
October 29
Speaker: Adam Giammarese (RIT)
Title: Decision Tree-Based Parameter-Free Method for Chaotic Time Series Forecasting
Abstract: Forecasting the future evolution of chaotic data-based systems is a crucial, but challenging practical problem. Existing solutions - such as Recurrent Neural Networks (RNNs) or Reservoir Computing (RC) - have been shown to be effective methods of forecasting time series, but require a slew of parameters and hyperparameters. In this work, we discuss a mostly parameter-free machine learning approach to chaotic time series forecasting and feature selection in the form of an Extra-Trees Regressor (ETR), which utilizes an ensemble of regression trees. We develop a method involving ETR that provides a notable performance in forecasting the future evolution of chaotic time series with limited information about the system itself. Using temporal systems such as the Rossler System, we demonstrate the efficacy of the developed forecasting method. The ETR-based forecast method is also applied to various (and more difficult to predict) systems, such as the spatio-temporal Kuramoto–Sivashinsky system. In comparison to the existing RNN and RC methods, we observe that our method provides comparable (if not impressive) performance while requiring far fewer parameters and hyperparameters that traditionally make the former systems difficult to use in practice.
November 5
Speaker: Quinn Kolt
Title: Constructing Unitary Fusion Category Representations with the Jellyfish Algorithm
Abstract: The graphical calculus is a modern technique for classifying and constructing “unitary fusion” categories, categories which model elementary particles that merge and split. In particular, if one can obtain enough diagrammatic relations to evaluate all “closed” diagrams, this graphical calculus uniquely describes the category. However, in order to prove existence, one must also find a representation of the category. Cuntz algebras, a type of C*-algebra, are a natural home for the representations of many fusion categories. The Jellyfish algorithm allows us to use diagrams to find what these Cuntz algebra representations should be in an intuitive way. Using this computation, we can then prove existence by showing that this construction is indeed a well-defined representation in the associated Cuntz algebra. In this talk, I will apply this process on the unitary fusion category with Fibonacci fusion rules.
November 12
Speaker: Yutong Wu
Title: Failed Positive Semidefinite Zero Forcing
Abstract: Given a simple, undirected graph $G$, consider each vertex in $V(G)$ as either “filled” or “unfilled”. Let $S$ be the set of vertices that are filled. The positive semidefinite zero forcing rule is as follows:
- Consider each component of $G-S$.
- For each component $G_i$ of $G-S$, consider $G_i+A$, where $A$ is the set neighbors of the vertices in $G_i$ from $S$.
- Apply zero forcing color change rule to $G_i+A$. That is, an unfilled vertex $v$ is forced to be filled if it is the only unfilled neighbor of a filled vertex.
The maximum size of a set of filled vertices that fails to fill all vertices of $G$ while applying the positive semidefinite zero forcing rule, denoted by $F^+(G)$, is called the failed positive semidefinite zero forcing number. We will discuss the parameter $F^+(G)$ for different types of graphs, as well as characterization of graphs with large $F^+(G)$ and graphs with small $F^+(G)$.
November 19
Speaker: Matt Coppenbarger
Title: An Impartial Combinatorial Game on a $3\times 3$ Board with Magic Square Constraints
Abstract:Two players, Alice and Bob (with Alice moving first), alternate on choosing an integer from $0$ to $n$ (inclusive) and entering the number into an empty space on an initially empty $3\times 3$ array with repetition allowed but subject to the constraints given in a magic square. Even though each games ends in at most nine moves, determining the player with the winning strategy is a surprisingly challenging and elusive problem. A complete solution is presented.
February 15
Speaker: Brendan Rooney
Title: The Colin de Verdière Number of a Graph.
Abstract: This talk is the first in a series of two talks on "strong" matrix conditions. In this talk we define the >Colin de Verdière graph invariant, and show that it is a minor monotone parameter.>
The Colin de Verdière number of graph $G$ is the maximum multiplicity of $0$ as an eigenvalue over matrices compatible with the adjacency matrix of $G$. In order for $M$ to be compatible with $G$ it must (among other things) satisfy the Strong Arnold Hypothesis. Our focus will be on this property, how it can be interpreted, and how it is applied. We will also discuss the characterization of planar graphs by their Colin de Verdière number. >Our discussion follows van der Holst, Lovász, and Schrijver (The Colin de Verdière graph parameter, 1997).
February 22
Speaker: Brendan Rooney
Title: The Strong Spectral Property and the Strong Multiplicity Property.
Abstract: This talk is the second in a series of two talks on "strong" matrix conditions. In this talk we focus on two analogous properties to the Strong Arnold Property, and their connection to the minimum number of distinct eigenvalues of a graph.
For a graph $G$ on $n$ vertices, $\mathcal{S}(G)$ is the space of $n\times n$ symmetric matrices whose off-diagonal zero pattern exactly matches that of $A(G)$. We are interested in finding $q(G)$, the minimum number of distinct eigenvalues of a matrix $M\in\mathcal{S}(G)$. A matrix $M$ has the Strong Spectral Property (SSP) if a pair of manifolds associated with $M$ intersect transversally at $M$. We will unpick what this means, and see how it can be used to give a lower bound of $q(G)$. Our discussion follows two papers of Barrett et al., "Generalizations of the Strong Arnold Property and the minimum number of distinct eigenvalues of a graph" (2016), and "The inverse eigenvalue problem of a graph: Multiplicities and minors" (2017).
March 1
Speaker: Shahla Nasserasr
Title: >A Nordhaus-Gaddum conjecture on the eigenvalues of graphs and their structures.
Abstract: For a graph $G$ on $n$ vertices, and a parameter $p$ related to $G$, a Nordhaus-Gaddum type problem is to find an upper bound and a lower bound as functions of $n$ for $p(G)+p(\overline{G})$. When $p(G)=q(G)$, the minimum number of distinct eigenvalues of $G$ (introduced in the previous talk by Dr. Rooney), it is conjectured that the upper bound is $n+2$. The conjecture is proved for many families of graphs. In this talk, we will focus on this conjecture and the families of graphs for which the conjecture is true. The talk will be out of this paper.
March 8
Speaker: Shahla Nasserasr
Title: Orthogonal matrices with a given pattern of zero entries.
Abstract: For a given graph $G$, let $S(G)$ be the set of all symmetric matrices such that the $(i,j)$ entry with $i\neq j$< is zero exactly when $ij$ is not an edge of $G$. The case when $S(G)$ contains an orthogonal matrix is especially interesting because that means $G$ has two distinct eigenvalues ($q(G)=2$). It is known that for any two connected graphs with the same number of vertices there is a symmetric orthogonal matrix compatible with their join. This statement is generalized by Levene et al. to graphs that are not necessarily connected. In this talk, we will focus on this generalization in the paper: https://arxiv.org/abs/2012.12694
March 15
Speaker: Darren Narayan
Title: Orthogonal matrices with zero diagonal.
Abstract: A presentation will be given on the paper "On orthogonal matrices with zero diagonal" by R. Bailey and R. Craigen. In this paper the authors consider real orthogonal $n\times n$ matrices whose diagonal entries are zero and off-diagonal entries nonzero. They use these results to determine the minimum number of distinct eigenvalues of matrices associated with some families of graphs, and consider the related notion of orthogonal matrices with a partially-zero diagonal.
March 29
Speaker: Bonnie Jacob
Title: Relating linkages to the inverse eigenvalue problem on a graph.
Abstract: In this talk, we will describe the results presented in Rigid linkages and partial zero forcing by Ferrero et al. (2019). We will discuss linkages and rigid linkage forcing. We will also explore how these concepts relate to matrix eigenvalue multiplicities.
April 5
Speaker: Louis Deaett (Quinnipiac University)
Title: Matroids and the minimum rank problem for matrices.
Abstract: Suppose the only information we have about a matrix is its number of rows, its number of columns, and whether each entry is zero or nonzero. What can this tell us about the rank of the matrix? This is a well-studied question in combinatorial matrix theory. In this talk, we discuss how to place this problem within the context of matroid theory, which can be thought of as a purely combinatorial abstraction of the way linear independence and rank behave over a vector space. We will revisit some known results and show how they can be better understood in terms of matroids. We will also use the connection to matroid theory to explain and improve on some existing examples, obtain a couple of new results, and highlight some new research questions opened up by this connection.
April 12
Speaker: Victoria McGraw
Title: Spanning Shallow-Light Trees.
Abstract: Shallow-Light Trees are a form of bicriteria optimization combining minimum weight spanning trees and shortest path graphs. Spanning Shallow-Light Trees are the simplest form of this optimization. However, the extensions and variations of Shallow-Light Trees are often applied to network optimization areas such as buy-at-bulk, routing topology, and data allocation problems. This presentation will provide an introduction and overview of the applications and construction of Spanning Shallow-Light Trees.
April 19
Speaker: Jobby Jacob
Title: Graphs with two distinct eigenvalues.
Abstract: We will discuss some of the results from the paper by Chen, Grimm, McMichael and Johnson, Undirected graphs of Hermitian matrices that admit only two distinct eigenvalues. In particular, we will discuss construction techniques used in this paper to study graphs where one of the two eigenvalues has multiplicity two.
April 26
Speaker: Noah Collins
Title: Extremal Graph Theory and Spectral Radii.
Abstract: One area of extremal graph theory involves looking at graphs being embedded in certain surfaces. From the paper Three Conjectures In Extremal Spectral Graph Theory, the authors show the structure of planer and outer planar graphs when embedded in the plane. In particular, the authors look at the spectral radii of outer planar and planer graphs. By looking at these graphs' spectral radii and maximizing the authors are able to deduce the structure of outer planar and planar graphs when embedded in the plane.
September 18
Speaker: Stanisław Radziszowski
Title: Chromatic Vertex Folkman Numbers
Abstract: For graph $G$ and integers $a_1 \ge \cdots \ge a_r \ge 2$, we write $G \rightarrow (a_1 ,\cdots ,a_r)^v$ if and only if for every $r$-coloring of the vertex set $V(G)$ there exists a monochromatic $K_{a_i}$ in $G$ for some color $i \in \{1, \cdots, r\}$. The vertex Folkman number $F_v(a_1 ,\cdots ,a_r; s)$ is defined as the smallest integer $n$ for which there exists a $K_s$-free graph $G$ of order $n$ such that $G \rightarrow (a_1 ,\cdots ,a_r)^v$. It is well known that if $G \rightarrow (a_1 ,\cdots ,a_r)^v$ then $\chi(G) \geq m$, where $m = 1+ \sum_{i=1}^r (a_i - 1)$. In this paper, we study Folkman graphs $G$ with chromatic number $\chi(G)=m$, which leads to a new concept of chromatic Folkman numbers. We prove constructively some existential results, among others, that for all $r,s \ge 2$ there exist $K_{s+1}$-free graphs $G$ such that $G \rightarrow (s,\cdots_r,s)^v$ and $G$ has the smallest possible chromatic number $r(s-1)+1$ with respect to this property. Among others we conjecture that for every $s \ge 2$ there exists a $K_{s+1}$-free graph $G$ on $F_v(s,s;s+1)$ vertices with $\chi(G)=2s-1$ and $G\rightarrow (s,s)^v$.
The paper and slides for this talk are available at #1 here.
September 25
Speaker: Brendan Rooney
Title: Efficient Domination in Regular Graphs
Abstract: A function $f:V(G)\rightarrow\{0,\ldots,j\}$ is an efficient $(j,k)$-dominating function on $G$ if $\sum_{u\in N[v]}f(u)=k$ for all $v\in V(G)$ (here $N[v]=N(v)\cup\{v\}$ is the closed neighbourhood of $v$). Efficient $(j,k)$-domination was introduced by Rubalcaba and Slater (2007) as a generalization of perfect domination, and efficient $k$-domination. We look at efficient domination on regular graphs, applying some standard tools from linear algebra and algebraic graph theory. Using these ideas we give a partial characterization of the values $k$ for which the Hamming graphs $H(q,d)$ are efficiently $(1,k)$-dominatable. This extends the theorem of Tietavainen-van Lint-Leont’ev-Zinov’ev characterizing codes that meet the sphere packing bound.
October 2
Speaker: Bonnie Jacob
Title: Minimum Zero-Diagonal Rank and Failed Skew Zero Forcing of Graphs
Abstract: Associated with any simple graph $G$ is a family of symmetric zero-diagonal matrices with the same zero-nonzero pattern as the adjacency matrix of $G$. There is a strong connection between the ranks of these matrices and the generalized cycles that exist as subgraphs of $G$. In this talk, we characterize all connected graphs $G$ with minimum rank of $3$ or below, as well as all connected graphs with minimum rank of $n$, the order of the graph. It turns out that the minimum rank is the order of the graph if and only if $G$ has a unique generalized cycle, also known as a unique perfect $[1,2]$-factor, among other names. We present an algorithm for determining whether a graph has a unique spanning generalized cycle. We also determine the maximum zero-diagonal rank of a graph, which is also related to generalized cycles, and then show that there exist graphs $G$ for which some ranks between minimum rank and the maximum rank of $G$ cannot be realized.
Related to the notion of minimum rank is the idea of zero forcing. For minimum zero-diagonal rank, the skew zero forcing number and failed skew zero forcing number provide bounds on the rank of a graph. We present some results for the failed skew zero forcing number of a graph.
These results are based on joint work with C. Grood, L. Hogben, J. Harmse, T. J. Hunter, A. Klimas, S. McCathern, T. Ansill, J. Penzellna, and D. Saavedra. Paper.
October 9
Speaker: Darren Narayan
Title: Symmetry in Point-Block Incidence Graphs
Abstract: We present infinite families of graphs $G$ where all symmetries can be removed by fixing a single vertex. That is, mapping any vertex to itself results in the trivial automorphism. These graphs, called point-block incidence graphs, lie at the intersection of graph theory and combinatorial design theory. A point-block incidence graph is a bipartite graph $G=(P,B)$ with a set of point vertices $P=\{p_{1},p_{2},...,p_{r}\}$ and a set of blocks $B=\{B_{1},B_{2},...,B_{s}\}$ where $p_{i}\in P$ is adjacent to $B_{j}\in B\Leftrightarrow p_{i}\in B$. A vertex $v$ in a graph $G$ is fixed if it is mapped to itself under every automorphism of $G$. The fixing number of a graph $G$ is the minimum number of vertices, when fixed, fixes all of the vertices in $G$ and was introduced by Laison, Gibbons, Erwin, and Harary.
We present infinite families of graphs with a fixing number of $1$, and further fixing any vertex fixes every vertex of the graph. We also show that other point-block incidence graphs can have a high degree of symmetry and a large fixing number as they can be expressed as the disjoint union of copies of $P_{2}\times P_{n}$, $K_{3,3}$, or Möbius ladder graphs. This is joint work with Josephine Brooks, Alvaro Carbonero, Joseph Vargas, Rigoberto Flórez, and Brendan Rooney.
October 16
Speaker: Kristijan Tabak (RIT Croatia)
Title: An Algebraic Proof That the Binary Fano Plane is Almost Rigid
Abstract: The existence of a binary $q$-analog of a Fano plane is still unknown. Kiermaier, Kurz and Wassermann proved that automorphism group of a binary $q$-analog of a Fano plane is almost trivial, it contains at most two elements. The method used there involved Kramer - Masner method together with an extensive computer search. In this paper we provide an algebraic (computer free) proof that automorphism group of a binary $q$-analog of a Fano plane contains at most two elements. We used group theory with calculations in a suitable group rings.
October 23
Speaker: Daniela Elizondo and Henry Fleischmann
Title: Efficient $(j,k)$-Domination on Chess Graphs
Abstract: Graphs defined by the legal moves of a chess piece are a classical setting for efficient domination. For a graph $G$, a function $f: V(G) \rightarrow \{0, 1, \ldots, j \}$ is an efficient $(j,k)$-dominating function if, for all $v \in V(G)$, $\sum_{w \in N[v]} f(w) = k$, where $N[v]$ is the closed neighborhood of $v$ (introduced by Rubalcaba and Slater, 2007).
We completely characterize efficient $(j,k)$-domination on King's graphs. This result generalizes to a construction that shows $G\boxtimes H$ is efficiently $(j,k)$-dominatable if and only if both $G$ and $H$ are. Additionally, we describe several necessary conditions for efficient $(j,k)$-domination, following our observations on Bishop's graphs.
On the torus, the Queen's and Bishop's graphs are realizable as Cayley graphs. We apply character theory to calculate the spectra of these graphs, through which we determine their efficient $(j,k)$-dominating functions.
For the standard $n\times n$ Queen's graph, we exploit an equitable partition to show computationally that, for $4 \leq n \leq 571$, efficient $(j,k)$-domination occurs only when $n = 10$. Expanding this approach, we construct an infinite class of graphs with an efficient $(j,k)$-dominating function from analogous equitable partitions.
October 30
Speaker: Shahla Nasserasr
Title: Achievable Multiplicity Partitions of a Graph
Abstract: For a graph $G$, the class of real-valued symmetric matrices whose zero-nonzero pattern of off-diagonal entries is described by the adjacencies in $G$ is denoted by $S(G)$. The inverse eigenvalue problem for the multiplicities of the eigenvalues of $G$ is to determine for which ordered list of positive integers $m_1\geq m_2\geq \cdots\geq m_k$ with $\sum_{i=1}^{k} m_i=|V(G)|$, there exists a matrix in $S(G)$ with distinct eigenvalues ${\lambda_1,\lambda_2,\cdots, \lambda_k}$ such that $\lambda_i$ has multiplicity $m_i$. A related parameter is $q(G)$, the minimum number of distinct eigenvalues of a matrix in $S(G)$. We study graphs that can achieve two distinct eigenvalues ($q(G)=2$) with given multiplicities. This is joint work with the Discrete Mathematics Research Group of Regina.
November 6
Speaker: Nate Cahill
Title: Relaxing Balanced Graph Cuts Part 2
Abstract: In April, I showed how image segmentation can be thought of as a process of partitioning an image into a small number of subsets, and how image segmentation algorithms can often be modelled as graph partitioning problems which are typically NP-hard. In this talk, we’ll focus on a particular instance of this algorithm, called “Balanced Cuts,” by describing the cost function whose minimum coincides with the optimal partitioning, and by showing how a relaxation of the discrete minimization problem yields a continuous problem that can be solved through a generalization of iteratively reweighted least squares (IRLS).
November 13
Speaker: John Whelan
Title: Mismatch Metrics, Lattice Coverings and Coordinate Choices: Adventures in the Parameter Space of Continuous Gravitational Waves>
Abstract: We describe the application of the lattice covering problem to the placement of templates in a search for continuous gravitational waves from the low-mass X-Ray binary Scorpius X-1.
Sco X-1 is a neutron star in a binary system with a low-mass companion star. It is believed to be rapidly spinning and a promising source of continuous gravitational waves. The signal received by an observatory such as LIGO, Virgo or KAGRA depends on the parameters of the system, and a search for that signal loses sensitivity if the incorrect values are used for those parameters. Several of the parameters (rotational frequency, projected orbital radius, orbital period and orbital phase) are uncertain, and one method to ensure that the signal is not missed is to perform the search at each point in a lattice covering the relevant parameter space.
The loss of signal-to-noise ratio (SNR) associated with an incorrect choice of parameters is, in a generic Taylor expansion, a quadratic function of the parameter offsets. This allows us to write the fractional loss in SNR, also known as the mismatch, as a distance using a metric on parameter space. In general, this metric will vary over the parameter space (i.e., the associated geometry will have intrinsic curvature), but we can divide the parameter space into small enough pieces that the space is approximately flat, and the metric can be assumed to be constant. In that case, there exists a transformation to Euclidean coordinates. The problem of placing templates so that the mismatch of any point in parameter space from the nearest template is no more than some maximum mismatch $\mu$ is then equivalent to the problem of covering the corresponding Euclidean space with spheres of radius $\mu$. The most efficient covering lattice in $n\le 5$ dimensions is the family $A_n^*$, which includes the hexagonal lattice $A_2^*$ and the body-centered cubic lattice $A_3^*$. For example, the density of lattice points for $A_4^*$ is a factor of $2.8$ lower than the corresponding hypercubic ($\mathbb{Z}^4$) lattice.
We use the LatticeTiling module in the LIGO Algorithms Library (lalsuite) to investigate efficient lattice coverings for the parameter space of a search for Sco X-1 using advanced LIGO data. We show how the search can be made more efficient by 1) replacing a hypercubic grid with an $A_n^*$ lattice, 2) accounting for the elliptical boundaries associated with the correlated prior uncertainties between orbital period and orbital phase, and 3) defining a "shearing" coordinate change such that a particular combination of the orbital period and orbital phase is "unresolved", and explicitly searching only in the other three dimensions of the parameter space. These improvements allow the search to be carried out using fewer computational resources. Alternatively, since the search method we use is "tunable", with a tradeoff between
computational cost and sensitivity, the more efficient lattice allows a more sensitive search to be done at the same computing cost.
This work is a collaboration between AST PhD student Katelyn Wagner and myself, with help from AST PhD student Jared Wofford.
November 20
Speaker: Rigoberto Florez
Title: Some Enumerations on Non-decreasing Dyck Paths
Abstract: A Dyck path is a lattice path in the first quadrant of the $xy$-plane that starts at the origin and ends on the $x$-axis. It consists of the same number of North-East ($U$) and South-East ($D$) steps. A pyramid is a subpath of the form $U^nD^n$. A valley is a subpath of the form $DU$. The height of a valley is the $y$-coordinate of its lowest point. A Dyck path is called non-decreasing if the heights of its valleys form a non-decreasing sequence from left to right.
In this talk, we count several aspects of non-decreasing Dyck paths. We count, for example, the number and weight of pyramids and numbers of primitive paths. In the end of the talk we introduce the concept of symmetric pyramids and count them. Throughout the talk, we give connections (bijective relations) between non-decreasing Dyck paths with other objects of the combinatorics. Some examples are, words, trees, polyominoes. This is a joint work with Eva Czabarka, José L. Ramírez, and Leandro Junes.
February 12
Speaker: Brendan Rooney
Title: An Introduction to Cayley Graphs
Abstract: Cayley graphs are graphs constructed from groups. We show how questions about graph symmetry naturally lead to Cayley graphs. We also survey some classical results about Cayley graphs.
February 19
Speaker: Brendan Rooney
Title: More Cayley Graphs
Abstract: We continue our discussion of Cayley graphs, shifting our focus to structural questions. We will look at cliques, neighborhoods, colorings, and more!
February 26
Speaker: Bonnie Jacob
Title: Construction of Graphs That Swap Distance-One and Distance-Two Pairs of Vertices
Abstract: The distance $d_G(u,v)$ between vertices $u$ and $v$ in a graph $G$ with vertex set $V(G)$ is the number of edges on a shortest path from $u$ to $v$. From a graph $G$, suppose we want to construct a new graph $H$ that has the same vertex set of $G$, but $d_{H}(u,v) = 1$ if and only if $d_G(u,v)=2$, and $d_{H}(u,v) = 2$ if and only if $d_G(u,v)=1$. For most choices of $G$, we would be out of luck. However, if $G=C_5$, for example, we can find such a graph $H$. In fact, $H=G=C_5$.
In this talk, we will discuss the motivation for considering this property and the conditions under which it holds.
March 18
Speaker: Brendan Rooney
Title: Hardness of Finding Maximum Cliques in Cayley Graphs
Abstract: Computing the clique number of a general graph is well-known to be NP-Hard. Codenotti et al. [Bruno Codenotti, Ivan Gerace, and Sebastiano Vigna. Hardness results and spectral techniques for combinatorial problems on circulant graphs. Linear Algebra Appl., 285(1-3): 123--142, 1998] showed that computing clique number and chromatic number are still NP-Hard problems for the class of circulant graphs. This result demonstrates that the assumption of vertex transitivity does not make computing clique numbers or chromatic numbers easier. It also raises the question of whether there are classes of Cayley graphs for which these problems are easy to solve.
We outline proof that computing clique number is NP-Hard for the class of Cayley graphs for the groups $G^n$, where $G$ is any fixed finite group. In particular, this shows that these problems are NP-Hard for cubelike graphs. Our method brings together: a construction for embedding graphs in Cayley graphs; quotients of groups; quotients of graphs; and, Goppa codes.
March 25
Speaker: Nishant Malik
Title: Networks based analysis of regional and global climate systems
Abstract: Analysis of large-scale spatiotemporal datasets of various regional and global climate phenomena is a challenging task, a recently developed innovative way to analyze these datasets is employing methods of network science. These methods are especially useful in situations where the underlying motivation for the analysis is identifying connectivity patterns between various dynamical features of the climate system. For example, using these methods, we can answer questions such as the role of ENSO (El Niño–Southern Oscillation) in global rainfall patterns.
In this talk, I will illustrate the effectiveness of network science-based climate data analysis by applying it to rainfall patterns over South Asia and East Asia. For monsoon over South Asia, I will show that we can identify various spatial patterns that precede extreme rainfall, these patterns can not only be used as early warning signs for extreme rainfall events but can also provide insights into various dynamical features of monsoon. Furthermore, for the East Asian region, using the community detection algorithm, we delineate regions of coherent rainfall during different seasons. Time permitting, I will show some of our recent work on predicting monsoon and ENSO using network analysis.
April 1
Speaker: Manuel Lopez
Title: Finding polynomials for functions modulo a prime with a little help from linear algebra>
Abstract: Every function $f:\mathbb{Z}/p\mathbb{Z}\rightarrow\mathbb{Z}/p\mathbb{Z}$, where $p$ is a prime, can be expressed as a polynomial. There wasn't any easily computable approach I could find, so I worked out one approach. I will also motivate why such a computational tool is useful for number-theoretic purposes.
April 8
Speaker: Darren Nararyan
Title: Graph theory metrics for analyzing functional MRI data and brain connectivity
Abstract: In recent years metrics from the theory of graphs and networks have emerged as powerful means for analyzing functional MRI data. These include an array of properties found commonly applied to the realm of transportation and social networks, such as the characteristic (average) path length, the clustering coefficient, as well as global and local efficiency. We have also focused on the concept of betweenness centrality, which measures the frequency in which shortest paths between regions pass through a particular region or connection. The talk will include an overview of these methods and show how they can be applied to analyze brain connectivity.
April 15
Speaker: Matthew Coppenbarger
Title: An Introduction to Combinatorial Game Theory
Abstract: Combinatorial Game Theory is based on a simple and intuitive recursive definition of games, which yields a very rich algebraic structure: games can be added and subtracted in a very natural way, forming an abelian group with a partial ordering. The talk will also introduce some of the fundamental games that motivate the theory.
April 22
Speaker: Nathan Cahill
Title: Relaxing Balanced Graph Cuts
Abstract: In the computer vision community, a huge focus of research over the last generation has been on analyzing and understanding images. One common “low-level” image analysis task, image segmentation, aims to partition an image into a small number of subsets that can be input into subsequent high-level image understanding tasks. In this talk, we’ll explore how image segmentation algorithms can often be modeled as graph partitioning problems which are typically NP-hard, and then we’ll discuss how some of these problems can be relaxed to generate heuristics that can be solved rapidly.
April 29
Speaker: Stanislaw Radziszowski
Title: Bounds on Shannon Capacity and Ramsey Numbers from Product of Graphs
Abstract: We study the Shannon capacity of channels in the context of Ramsey numbers. We overview some of the results on channel capacity, and how Ramsey-type constructions may enhance them. A new lower bound for a special type of multicolor Ramsey numbers is presented, which implies that the supremum of the Shannon capacity over all graphs with independence 2 cannot be achieved by any finite graph power. This generalizes to graphs with any bounded independence number.
The paper and slides are available at #33 here.
September 25
Speaker: Brendan Rooney
Title: Hedetniemi's Conjecture: Past, Present, and Future
Abstract: In 1966 Stephen Hedetniemi conjectured that the chromatic number of the direct product of graphs $G$ and $H$ is equal to the minimum of the chromatic numbers of $G$ and $H$. In the 53 years it has stood open, this conjecture has inspired a great deal of research on graph colourings and homomorphisms. Very recently (May of 2019!), Yaroslav Shitov published a construction on the arXiv giving counterexamples to Hedetniemi's Conjecture. I will give an introduction to this conjecture, some evidence for its validity, an account of Shitov's construction, and some results that suggest further directions for research.
October 9
Speaker: Stanisław Radziszowski
Title: On a Diagonal Conjecture for Classical Ramsey Numbers
Abstract: Let $R(k_1,\ldots,k_r)$ denote the classical $r$-color Ramsey number for integers $k_i\geq 2$. The Diagonal Conjecture (DC) for classical Ramsey numbers poses that if $k_1,\ldots,k_r$ are integers no smaller than $3$ and $k_{r-1}\leq k_r$, then $R(k_1,\ldots,k_{r-2},k_{r-1}-1,k_r+1)\leq R(k_1,\ldots,k_r)$. We obtain some implications of this conjecture, present evidence for its validity, and discuss related problems.
Let $R_r(k)$ stand for the $r$-color Ramsey number $R(k,\ldots,k)$. It is known that $\lim_{r\rightarrow\infty}R_r(3)^{1/r}$ exists, either finite or infinite, the latter conjectured by Erdős. This limit is related to the Shannon capacity of complements of $K_3$-free graphs. We prove that if (DC) holds, and $\lim_{r\rightarrow\infty}R_r(3)^{1/r}$ is finite, then $\lim_{r\rightarrow\infty}R_r(k)^{1/r}$ is finite for every integer $k\geq 3$.
Paper: arxiv.org/abs/1810.11386.
Slides: ram19a.pdf.
October 23
Speaker: Bonnie Jacob
Title: Results and Remaining Questions About Failed Zero Forcing on Directed Graphs
Abstract: Let $D$ be a simple digraph (directed graph) with vertex set $V(D)$ and arc set $A(D)$ where $n=|V(D)|$, and each arc is an ordered pair of distinct vertices. If $(v,u) \in A(D)$, then $u$ is considered an out-neighbor of $v$ in $D$. Initially, we designate each vertex to be either filled or empty. Then, the following color change rule (CCR) is applied: if a filled vertex $v$ has exactly one empty out-neighbor $u$, then $u$ will be filled. The process continues until either all of the vertices in $V(D)$ are filled, or the CCR restricts the remaining empty vertices from being filled. If all vertices in $V(D)$ are eventually filled, then the initial set is called a zero forcing set (ZFS); if not, it is a failed zero forcing set (FZFS).
In this talk, we define the failed zero forcing number $\operatorname{F}(D)$ on a digraph, which is the maximum cardinality of any FZFS. The zero forcing number, $\operatorname{Z}(D)$, is the minimum cardinality of any ZFS. We characterize oriented graphs that have $\operatorname{F}(D)<\operatorname{Z}(D)$ and present a list of digraphs with the same property. We also characterize digraphs with high and low values of $\operatorname{F}(D)$. We also discuss some open questions that remain about failed zero forcing on directed graphs.
This is based partially on work during the 2018 REU together with Alyssa Adams of Youngstown State University.
November 6
Speaker: Darren Narayan
Title: The Asymmetric Index of a Graph
Abstract: A graph $G$ is asymmetric if its automorphism group is trivial. Asymmetric graphs were introduced by Erdős and Rényi (1963). They suggested the problem of starting with an asymmetric graph and removing some number $r$ of edges and/or adding some number $s$ of edges so that the resulting graph is non-asymmetric. Erdős and Rényi defined the degree of asymmetry of a graph to be the minimum value of $r+s$. In this paper, we define another property that measures how close a given non-asymmetric graph is to being asymmetric. We define the asymmetric index of a graph $G$, denoted $ai(G)$, to be the minimum of $r+s$ so that the resulting graph $G$ is asymmetric.
We investigate the asymmetric index of both connected and disconnected graphs. We prove that for any non-negative integer $k$, there exists a graph $G$ where $ai(G)=k$. We show that the asymmetric index of a cycle with at least six vertices is two, and provide a complete characterization of all possible pairs of edges that can be added to a cycle to create an asymmetric graph. In addition we determine the asymmetric index of paths, certain circulant graphs, Cartesian products involving paths and cycles, and bounds for complete graphs, and complete bipartite graphs.
November 20
Speaker: Jobby Jacob
Title: On the Characterization of Graphs Based on Their Rank Numbers
Abstract: For a graph $G$, an onto function $f$ from the vertex set of $G$ to $\{1,2,\ldots,k\}$ is a $k$-ranking if $f(u)=f(v)$ implies that every $uv$-path contains a vertex $x$ such that $f(x)>f(u)=f(v)$. The rank number of a graph $G$ is the minimum value of $k$ such that $G$ has a $k$-ranking.
We will discuss the rankings of some classes of graphs, and in particular, we will discuss a recent result on characterizing graphs with large rank numbers.
December 4
Speaker: Matthew Coppenbarger
Title: Iterations of the Sisyphus Function
Abstract: The Sisyphus function is defined; and we determine the smallest non-negative integer $n$ requiring a specified number of iterations of the function that must be applied to $n$ until the sequence generated by the iterations of this function becomes stable or cycles.




